Split-step numerical method

The split-step method is a numerical method that can be used, for example, for finding a numerical solution of scalar Maxwell’s propagation equations having both linear and nonlinear terms. Each numerical step in the propagation direction is composed of applying two half-step linear operators (linear portions) and one one-step non-linear operator in between the linear portions towards a solution at a previous numerical step.

In the scalar form of Maxwell’s equations, the electric field of a cylindrical beam of light propagating in the z-direction can be written as

E(z,t) = φ(z,t) exp[ -iωt ]

However, the phase of φ(x,y,z,t) varies rapidly along the propagation direction (usually specified as the z-direction). This rapid phase variation is not important for many types of problems and can be removed by introducing a slowly varying field A(z,t) and constant k, such that

φ(z,t) = A(z,t) exp[ ikz ]

It is assumed that A(z,t) varies slowly in the propagation direction z as well as the other two directions and time t,

| ∂A/∂z | << k | A |
| ∂A/∂t | << ω | A |

which implies, for example, that

∂2A/∂z2 ≈ 0

This reduces a second order differential equation to a first order equation that is easier to solve.

∂A(z,r,t) /∂z = (L + N) A(z,r,t)

where L is comprised of linear terms (e.g., background absorption, diffraction and dispersion) and N is comprised of nonlinear terms (e.g., Kerr term, single- or multi-photon absorption). Applying both operators at once is not possible during numerical integration. An obvious shortcut will be to apply the operators in turn as follows

A(z + h,r)= exp[L h]   exp[N h]   A(z,r)

However, this may drastically decrease accuracy of the numerical solution as the linear and nonlinear operators do not commute:

exp[L + N] ≠ exp[L]   exp[N]

To achieve a better accuracy one can make splitting mode efficient (a variation of standard Strang splitting, second order accuracy):

exp[L + N] ≈   exp[L/2]   exp[N]   exp[L/2]

Assume the propagation direction is divided into increments of length h as shown below.


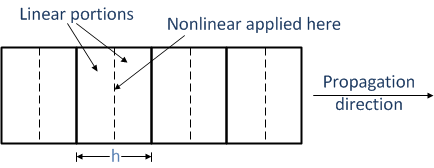
Split-step method diagram


For a propagation step of length h the solution of the differential equation at A(z + h) is

A(z + h, r) ≈   exp[L h/2]   exp[∫ N(z’) dz’]   exp[L h/2] · A(z,r)

The nonlinear portion for the entire increment h (the middle integral factor shown above) is applied at the center of the increment and between the two linear portions. The integral of N(z’) is calculated over the whole increment h from z’ = z to z’ = z + h.

Several variations of this method exist. Depending on the problem at hand (e.g., complexity of nonlinear or linear operators), one can surround the linear step with two nonlinear half-steps:

A(z + h, r) ≈   exp[N h/2]   exp[∫ L(z’) dz’]   exp[N h/2] · A(z,r)

A higher (fourth) order can be also applied as follows

A(z + h, r) ≈ SS2(ah) • SS2({1-2a}h) • SS2(ah) • A(z,r)

where SS2 (h) = exp(N h / 2) • exp ( ∫ L(z’) dz’) • exp (N h / 2) is a split-step operator of the second order and a=(2+21/3+2-1/3)/3 is a constant.



See also: Slowly varying envelope approximation (SVEA).

SimphoSOFT logo SimphoSOFT® mathematical model is based on applying a split-step method to a set of coupled propagation and rate equations.

SimphoSOFT® can be purchased as a single program and can be also configured with Energy Transfer add-on ET add-on, Multi-Beam add-on Multi-beam add-on, Optimization add-on Optimization add-on, Z-scan add-on Z-scan add-on, and MPA Info+ add-on MPA Info+ add-on for an additional charge. Please, contact our sales staff for more information
  • e-mail
  • phone: +1 (973) 621-2340
You can request a remote evaluation of our software by filling out online form -- no questions asked to get it, no need to install it on your computer.